The Human/AI Frontier: A Conversation with Bogdan Grechuk

‍tl;dr
At Surge AI, we work with the world’s sharpest minds to push the limits of AI. Professor Bogdan Grechuk—an IMO gold medalist and Associate Professor at the University of Leicester—is one of them. We interviewed him about the work he does to train SOTA models to perform frontier research.

Our vision: to build the world’s largest network of brilliant minds, collaborating to advance AI.

Meet Bogdan

‍Tell us a little about you and your research?

I’ve been obsessed with hard math problems since I was a teenager. Winning a gold medal at the International Mathematical Olympiad was a turning point—it showed me what’s possible when you dedicate yourself to solving the hardest questions. Today, I’m an Associate Professor of Mathematics at the University of Leicester. My research focuses on number theory, probability, and optimization, as well as their real world applications.

What’s a problem in your field that you care about most? Do you think AI might help?‍

I’m particularly fascinated by Diophantine equations. They’re problems that are simple enough to write in a single line, but often remain unsolved for centuries. A classic example is Fermat’s Last Theorem: one line, 350 years before it was finally cracked.

My vision is to work with AI in a loop to solve such problems. Whenever I invent a new method, I teach it to the model, and then the model quickly tests which other problems it can solve. I get to focus on new techniques, and AI does the testing and exploration.

How do you use AI in your research today, and what challenges do you see?

‍More and more, I rely on AI to handle the routine parts. When I wrote my book on Diophantine equations, everything had to be done by hand. Now, once I teach AI the method, it can handle the problem solving.

The issue is that models often produce answers that look convincing but are wrong. Instead of making me more productive, I waste time checking the work. I know this is a common problem in many fields, but in mathematics this should be easier to fix! We have formal proof systems that can verify the answer. If AI could get better at using such tools to check its work, it would be much more helpful, becoming a trustworthy research partner.

What’s an example of the work you’ve been doing with Surge?

‍One project I’ve been focusing on is creating and testing problems that are just beyond the capability of current models—questions they can’t solve yet, but should be able to if they were trained to recognize and implement the right methods.

Here’s an example that stumped every SOTA model:

For positive integer $n$, let $f(n)$ be the smallest positive integer $z$ such that the equation $x^3 + x y^2 - y^2 z + n y z^2 = 0$ has a solution in positive integers $x,y$. Let us also define $f(n) = 0$ if no such $z$ exists. Compute $f(n)$ for $n=1,2,3,4,5,6$, and then compute the sum $\sum_{n=1}^6 f(n)$.

All the SOTA models got it wrong. They approached it like a programmer with decent mathematical ability, rather than a mathematician. What I mean by that is they tried to write code to brute-force search for an answer, rather than reasoning about the deeper mathematical structure of the problem.

However, when I gave GPT-5 the steps of the correct method, it was able to work through them and get the correct answer. This shows that the capability is almost there, but the models need some guidance—just like a talented student.

See the appendix for Bogdan’s explanation of what three SOTA models – GPT-5, Gemini, and Claude – did wrong, and how he guided GPT-5 to the right answer.

Why do you work with Surge?‍

I get to work on the interesting parts of demanding problems while collaborating with other brilliant researchers. And it’s exciting knowing that I’m helping to build AI systems that I might one day use to solve the hardest challenges in my field.

‍

Appendix 

GPT-5

Part 1: GPT-5 jumps straight to brute-force

GPT-5 correctly identifies the problem as a Diophantine equation, but instead of considering established methods, it immediately defaults to brute force.

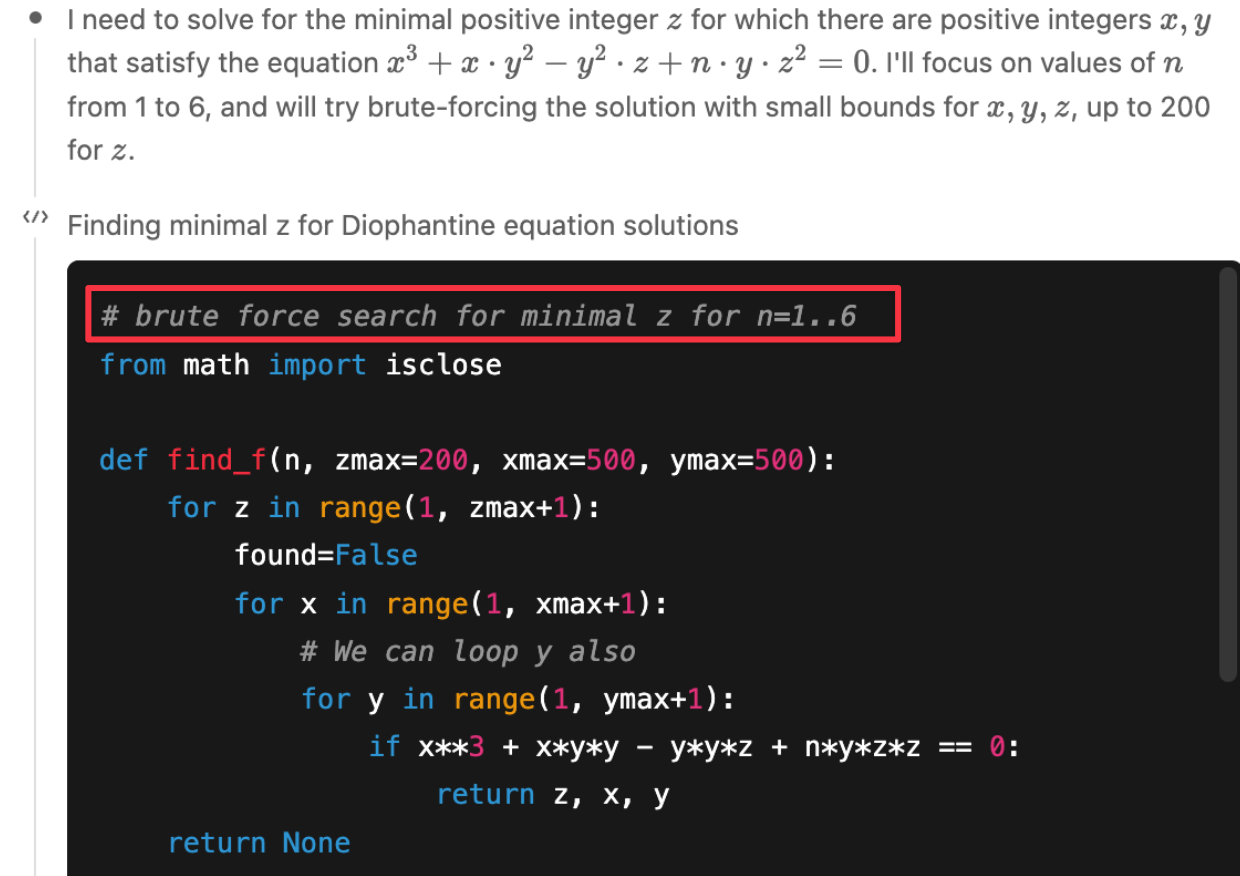
Part 2: GPT-5 applies some simple algebra

GPT-5 realizes brute-force would be too slow. It tries some algebraic simplifications but doesn’t pursue deeper mathematical methods or standard techniques for Diophantine equations. It does find the constraint $y > nz$, which narrows the search, but solving the problem requires much more advanced tools.

Part 3: GPT-5 looks for simple patterns

GPT-5 then notices some patterns in the solutions it has found so far. 

However, this fact doesn’t require brute-force search; it follows directly from the equation
$x^3 + x y^2 - y^2 z + n y z^2 = 0$.

Rearranging:

x3+y(xy−yz+nz2)=0⇒x3=y(−xy+yz−nz2).x^3 + y(xy - yz + nz^2) = 0 \quad \Rightarrow \quad x^3 = y(-xy + yz - nz^2).x3+y(xy−yz+nz2)=0⇒x3=y(−xy+yz−nz2).

Since $(-xy + yz - nz^2)$ is an integer, we conclude $y = kx^3$ for some integer $k$.

GPT-5 approaches this from the opposite direction of mathematicians: instead of analyzing the equation’s structure, it naively searches for solutions and only afterward tries to detect patterns.

Part 4: GPT-5 gets the wrong answer

GPT-5’s brute force search and pattern matching is not sufficient. Thus, it gives the incorrect final answer:

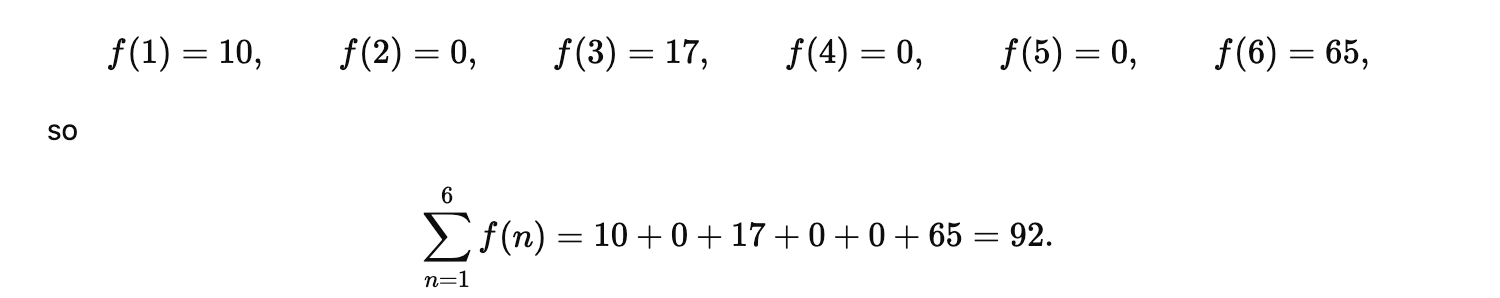
What about other models?

Claude Opus 4.1 and Gemini 2.5 Pro performed similarly: using brute-force, and getting an incorrect answer.

Claude Opus 4.1

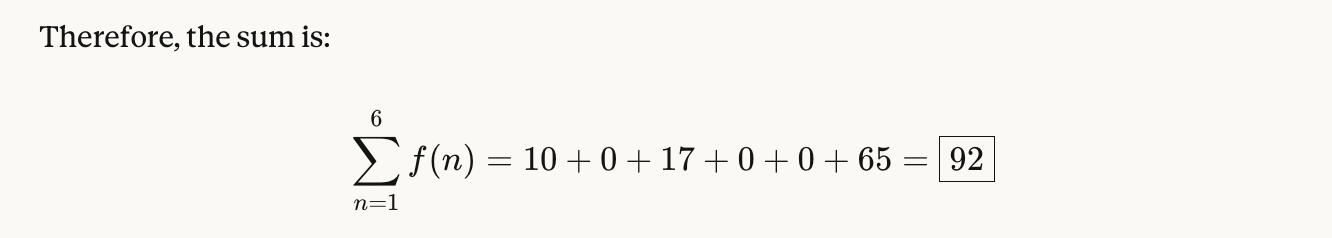
Gemini 2.5 Pro

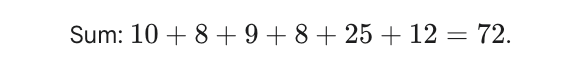
Guiding GPT-5 through the problem

Read Bogdan’s full conversation with GPT-5

After it failed the first attempt, I provided GPT-5 with the correct approach, namely:

• Transform the equation to an elliptic curve in Weyestrass form in homogeneous coordinates by a rational change of variables
• Find a rational point $P$ on the curve that is not a torsion point, then compute $kP$ for $k = \pm 1, \pm 2, \dots$. For each point, do the inverse transformation to obtain a solution $(x,y,z)$ to the original equation $x^3 + x y^2 - y^2 z + n y z^2 = 0$.
• Find a positive integer solution $(x,y,z)$ with minimal $z$, and use it to compute $f(2)$.
• Use the same method to compute f(4) and f(5)

With this guidance, GPT-5 was able to arrive at the correct solution. 

Other models

When given the same guidance, Opus 4.1 and Gemini 2.5 Pro were still unable to solve the problem.

The current capabilities of AI

So, right now, AI can win gold medals at the IMO, and even solve some PhD level problems with clear guidance. The next step will be AI that can solve research problems on its own, by applying known methods. Maybe one day it can even begin to contribute to the creation of new methods.